Fast ML for Funky Effects

Using domain inspired machine learning for embedded digital signal processing.

Date:
2025-09-07

I’ve recently become interested in building a digital guitar pedal. Specifically, I want to build a one-knob talking filter that would sound a bit like this:

0:00 / 0:00
Example of transient detector being used to modulate frequencies of a formant filter, resulting in a talking-guitar effect.

The talking effect comes from a formant filter being modulated in response to notes. To detect notes, I need a transient detector, a device that identifies rapid changes in audio amplitude or spectral content. Rather than allowing users to select these parameters (and compromise my minimal one-knob aesthetic), I used a learning algorithm to select a set of parameters based on data. This design is functionally a machine learning model with a less general set of basis functions. Compared to traditional ML techniques for signal processing, such as CNNs or LSTMs, this approach has the following advantages:

  1. Predictability: An audio effect that doesn’t do what the musician expects every time is worthless. Simpler models are less likely to overfit and even when the model is wrong, it will always be wrong in similar circumstances.
  2. Decreased resource utilization: My transient detector needs to run on an ESP32-S3 and still leave room for the main DSP algorithm, such as the filter effect. Using only 18 parameters and being based on conventional DSP techniques, it is possible to manually optimize the implementation for the most efficient resource usage.
  3. Less training data: Since this is a one-person hobby project, I didn’t want to spend a lot of time labeling training data. I manually labeled about 6 minutes of audio, which only took me a couple of hours.
  4. Explainability: Because the model is forced to take the shape of a classical algorithm, the learned parameters are directly interpretable and are always in real-world units (i.e., seconds or hertz).
  5. Global Optimization: Complex ML models are constrained to using local-minima search algorithms such as gradient descent. A very small model can be trained with global optimization techniques that take advantage of the whole parameter set.

The downside is accuracy, with my model achieving around 60% to 70% precision with similar recall. This may be due to the model’s limited ability to analyze frequency domain content of the input, something traditional models are more suited to.

Model Architecture

Schematic of a transient detector. The input first flows into a compressor which is marked optional. That flows into a group of envelops in parallel. One envelope is expanded. In it, the signal flows into an IIR bandpass filter or an FIR bandpass filter during training. Both filters are marked optional. Next, the signal is squared and either averaged using a sigmoid kernel or, if in inference mode, a rectangular kernel. The result of the average is square-rooted and a gain is applied, exiting the envelope block. The result of each envelope is summed with a bias, another gain is applied and the result flows to a sigmoid activation function. The result of that function is output.
Complete transient detector model architecture. A bank of envelope generators are weighted, summed and limited by a sigmoid activation function, mimicking the difference-and-threshold architecture of a classical transient detector. An optional compressor and per-channel bandpass filters can be enabled to allow the learning algorithm more flexibility in its solution.

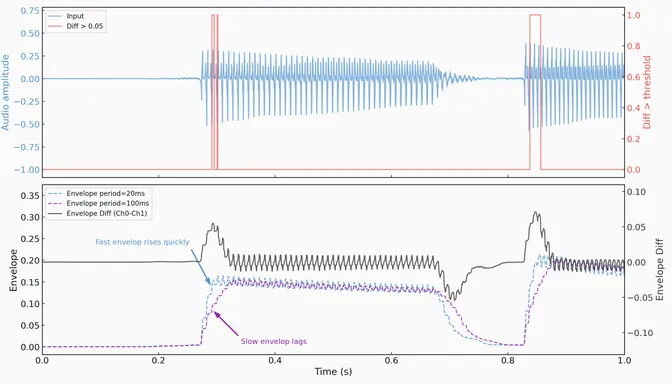
The classic transient detector algorithm uses a fast envelope generator and a slow envelope generator, which are subtracted to produce an estimate of how quickly the amplitude of the original signal is changing. When the input amplitude changes quickly, this difference exceeds a threshold and a note is detected.

Classical Transient Detector Operation
Classical Transient Detector Operation: This figure demonstrates the operating principle of a transient detector. The top subplot shows a guitar waveform and a thresholded difference signal. The bottom subplot displays 'fast' and 'slow' envelopes derived from the audio, highlighting how the fast envelope rises quickly while the slow envelope lags at the start of a note. The difference between these envelopes is used to detect the transient.
Operating principle of a transient detector applied to a guitar. The difference of the fast envelope and slow envelope can be seen to peak when a note starts.

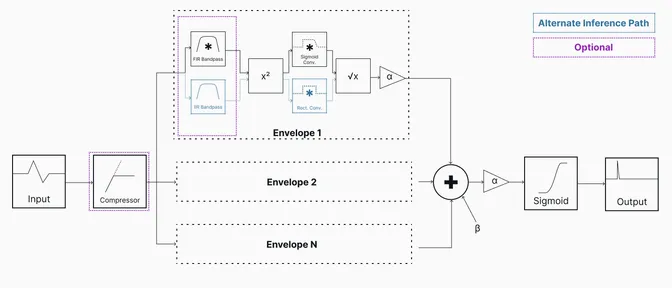
My model also uses a bank of envelope generators to estimate the signal’s amplitude, although the quantity is configurable rather than being fixed at two. Rather than differencing and thresholding the output, the model weights each envelope, sums them, and limits the output with a sigmoid function. By selecting appropriate weights and biases, the model is able to mimic the effect of the classical algorithm, although this architecture is more flexible. Replacing the threshold with a sigmoid function allows the model to be differentiable. For differentiability, the moving average is replaced by a smoothed version during training, but the simple moving average is retained during inference.

Two optional components are added to the model, enabled by hyperparameters. The first is an audio compressor, which helps normalize the overall level of the input. The time constant of the compressor’s internal envelope generator, the threshold, and the makeup gain are learnable parameters.

The second optional component is a per-channel bandpass filter to allow each envelope to focus on a specific region of the audio spectrum. Each filter has a learnable center frequency and Q (which controls the bandwidth). They are implemented as biquad IIR filters to allow for efficient inference on a microprocessor. However, this filter design is inefficient on a GPU, so, during training, an equivalent FIR filter is used.

Data & Learning

For training data, I used a collection of free stems, including recordings of guitar (both DI and distorted), kick drum, bass, and synthesizer. I listened for the start of each note and labeled it in Audacity. These labels are used to create a target signal which is zero everywhere except for the period starting at each transient and lasting 20ms, where it is one. The model attempts to reproduce this target signal.

Data Annotation
Screenshot of Audacity project displaying audio waveforms and spectrograms. The start of transient events on guitar and kick tracks are annotated using label tracks.
Label tracks are used to manually label transients in Audacity.

To optimize the parameters, traditional optimization techniques such as stochastic gradient descent and L-BFGS-B tend to stay too close to the initial conditions. Furthermore, these techniques don’t work well with differently scaled parameters, such as the filter cut-off (in hertz) and envelope time (in seconds). To solve this, I used global optimization techniques. Both basin-hopping with an analytic Jacobian and differential evolution were evaluated, with differential evolution giving the best results. Unlike stochastic gradient descent, these global optimization techniques require the entire training set to be included in a single batch. As the whole of the training data is only twenty 5-second audio clips, this is not a problem.

Training Loss
Training loss for multiple models. The differential evolution algorithm results in long plateaus while it searches for a new local minima, followed by rapid decreases where it exploits the new result. Early termination indicates the model could no longer improve.

Results

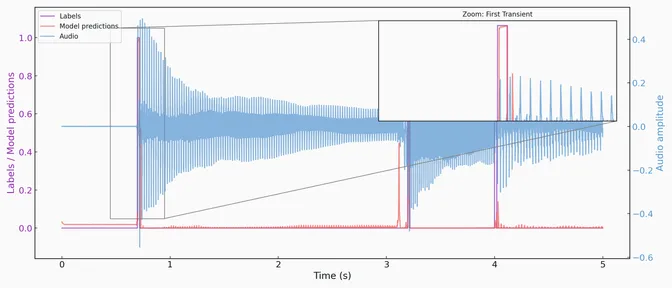
Model results on bass guitar: This figure displays an audio waveform, along with model predictions and labeled transients. The model's predictions (red line) closely align with the labeled transients (purple line). An unlabeled spike in the predictions occurs around the three second mark, with minimal change in the audio waveform.
Model results on a bass guitar using three channel model with filter and compressor. The red predictions line has been trained to mimic the purple labels line. The spike around three seconds that does not correspond with a label is a fret noise, which I choose not to label, but could have been.

I evaluated the model on a selection of audio clips not included in the training data. Rather than comparing to the target signal, the evaluation metrics are based on the phenomenon of interest, detecting a transient. Predictions are created from a rising edge detector with hysteresis on the model output and compared to ground truth. If a detection is within 20ms of the true value, a true positive is reported. If the detection is not within that window, a false positive is reported. Similarly, false and true negatives are computed.

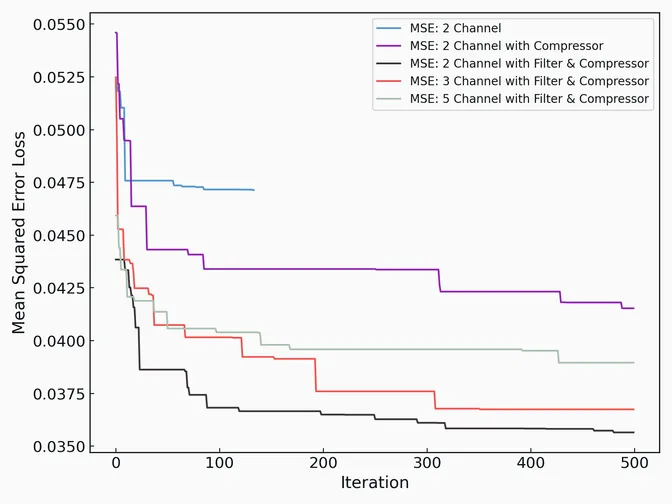
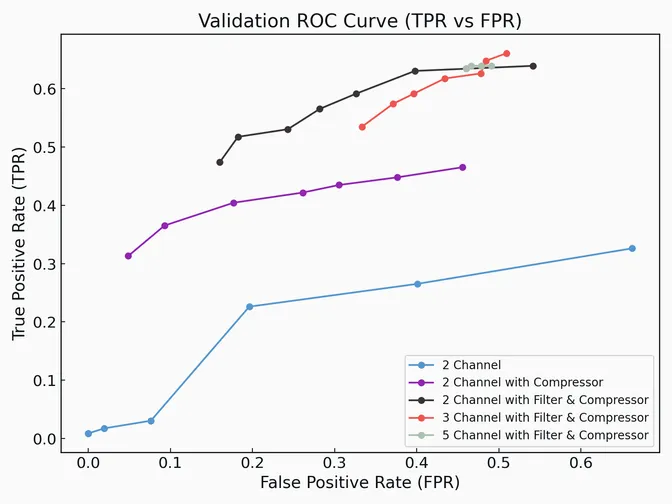
Overall, the model performed modestly, achieving 70% precision at 53% recall for the three-channel with compressor and bandpass filter case. Interestingly, increasing model complexity mostly assists with recall and not precision. I believe this is attributable to “hard” transients which involve a change in pitch without an accompanying change of amplitude. I did not use separate validation and test sets, partly because the design of the model is robust to overfitting, but more because this is a personal project and I did not want to spend too much time labeling data.

ROC curve for a selection of model architectures: This figure displays ROC curves for various model configurations, plotting True Positive Rate (TPR) against False Positive Rate (FPR). The true positive rate is maxed out at 0.6, while the minimum false positive rate increases with more complex models.
ROC curve for a selection of model architectures. Notice that the true positive rate is maxed out at 0.6, while the minimum false positive rate increases with more complex models.

The model generalized well enough to produce the audio clip at the beginning of this post. Future work involves improving model performance with a more advance architecture and implementing and profiling the design on hardware.

Call to action: If you would be interested in a series of well-tuned one-knob pedal effects that are always in the sweet-spot, reach out to me. They say it’s never to early to start doing market research, although I don’t have plans to commercialize any time soon.